Các nhà khoa học cho rằng, chỉ cần 8 con số là đủ cho môn Toán

Số học là một phân nghành toán học lâu đời và cổ xưa nhất, nó cũng là nền tảng sơ cấp cho sự phát triển của đại số sau này. Ra đời từ chính thực tế khách quan, khi loài người cần một "cái gì đó" để có thể đong đếm số lượng thú săn, hoa quả hái được.

Thế nhưng những con số mà chúng ta tưởng như vô cùng đơn giản và tự nhiên như 1 cộng 1 là 2 này lại có lịch sử phát triển lâu dài để hoàn thiện hệ thống số như ngày nay.

Toán học xây dựng từ 8 số nền tảng.

Trong đó mỗi nền văn minh lớn như Ai Cập, Lưỡng Hà, Babylon, Ấn Độ, Hy Lạp cổ đại,... đều có những đóng góp quan trọng cho sự hoàn thiện ấy. Một điều thú vị là số 0, con số tưởng như vô giá trị này lại chính là phát minh lớn nhất và cuối cùng trong hệ thống đó.

Ngày nay không ai có thể phủ nhận vai trò của những con số này trong cuộc sống hằng ngày. Thật khó hình dung ra cuộc sống sẽ như thế nào nếu không có những con số kỳ diệu này.

Hệ thập phân là hệ số sử dụng phổ biến nhất với 10 con số (0 đến 9), từ đó chúng ta có thể biểu diễn hàng chục hàng trăm rồi tới những con số lớn hơn chỉ từ 10 con số đó. Thế nhưng liệu đây có phải là tất cả những gì loài người cần để có thể làm toán?

Thật khó tin và cũng rất thú vị khi biết rằng toán học chỉ cần 8 con số thôi cũng đủ để loài người đạt tới sự phát triển như bây giờ. Vậy đó là những con số nào, hãy cùng khám phá nhé!

Số thứ nhất: Số 0 - số vô giá trị hay vô giá?

Số O có phải vô giá trị?

Đại diện cho tập hợp rỗng (không có gì) thế nhưng nó lại là phát minh cuối cùng trong hệ thống số và phải rất lâu sau mới được thêm vào, trở thành con số hoàn hảo cuối cùng cho bộ số ngày nay.

Số 0 đứng phía trước thì không có giá trị gì (như 09, 008) thế nhưng chỉ cần thay vị trí ra phía sau, chúng ta đã có những con số hoàn toàn khác (90, 800)

Số 0 cũng rất đặc biệt khi vừa là bội số của tất cả các số (số nào nhân với 0 cũng là 0), vừa là phần tử trung tính (số nào cộng với 0 cũng không thay đổi giá trị).

Ngoài ra trong đại số và số học, số 0 luôn được xếp ở giữa, chia trục số thành phần âm và dương. Đóng vai trò không hề nhỏ trong toán học và không thể thiếu được.

Số thứ hai: Số 1

Đây là phần tử trung tính đối với nhóm phép nhân (số nào nhân với 1 cũng không thay đổi giá trị), và từ 1 ta có thể xây dựng toàn bộ trục số tự nhiên (ví dụ 2 = 1 + 1, 3 = 1 + 1 +1,...).

Như vậy chỉ cần số 1 là chúng ta đã có các con số khác rồi!

Số thứ ba: -1 hay âm 1

Số 1 là số đơn vị.

Nếu chỉ từ 1, chúng ta có thể xây dựng toàn bộ trục số theo chiều dương (số tự nhiên) thì với trục số theo chiều âm (số âm), chúng ta có thể làm tương tự với "người anh em sinh đôi của nó": - 1!

Như vậy, với -1 ta cũng có thể xây dựng toàn bộ trục số nguyên âm như trên ( - 2 = -1 - 1 hoặc lấy số nguyên nhân với - 1 (- 2 = -1. 2).

Trong lịch sử phát triển của số học, số âm ra đời là do nhu cầu biều diễn những món nợ trong cuộc sống hằng ngày hay sự thâm hụt nào đó. Hay như những đại lượng có giá trị dưới 0 như nhiệt độ âm!

Số thứ tư: 1/10

Cũng theo sự phát triển của nhu cầu cuộc sống, số nguyên không thể đáp ứng những phép tính không nguyên như chia một cái bánh cho 3 người vậy. Do đó ra đời số hữu tỉ (ví dụ: 1/4 hay 2/7).

Thế nhưng cũng giống như cách xây dựng trên, chúng ta chỉ cần một số đơn vị đó là 1/10 để có thể xây dựng hệ thống số hữu tỉ.

Số thứ năm: Căn bậc của 2

Thế giới đa dạng của số học.

Sự phát triển không ngừng khiến chúng ta cần biểu diễn những đại lượng khác mà số hữu tỉ không thể biểu diễn được. Ví dụ cạnh huyền của một tam giác vuông cân có độ dài cạnh góc vuông là 1 (khi đó bằng công thức Pytagore ta tính được độ dài là căn 2).

Giá trị này là một số vô tỉ và xấp xỉ 1.41421356...

Số thứ sáu: Pi (π)

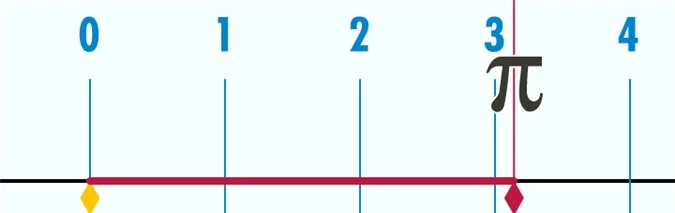
Mô tả trực quan số pi.

 

Đây là số vô tỉ khác có vai trò rất quan trọng trong hệ thống số, pi là giá trị của tỷ số giữa chu vi của một đường tròn với đường kính của đường tròn đó. Hằng số này có giá trị xấp xỉ bằng 3,14159265358979...

Điều khiến nó trở nên đặc biệt hơn số vô tỉ căn bậc 2 nói trên đó là pi là số vô tỉ đồng thời là số siêu việt (tức là nó không phải là nghiệm của bất kì đa thức với hệ số hữu tỉ nào).

Tính chất này cũng là lời giải cho bài toán cầu phương nổi tiếng hay chia 3 một góc, gấp đôi khối lập phương có nôi dụng như sau:

Dùng thước và compa dựng một hình vuông có diện tích bằng diện tích một hình tròn đã cho. Cũng như bài toán chia ba một góc và bài toán gấp đôi khối lập phương.

Số pi.

 

Các bài toán này đều không thể giải được vì sự tính chât siêu việt của số pi. Ngày nay, số pi xuất hiện trong mọi lĩnh vực của đời sống chứ không riêng gì toán học, nhất là vật lý như chu kỳ hàm sóng.

Số thứ bảy: Euler (e)

Số e xuất hiện trong giải tích.

Một hằng số toán học nổi tiếng và quan trọng không kém chính là số e (cơ số của logari tự nhiên). Tên của nó được đặt tên theo nhà toán học nổi tiếng người Thụy Sĩ Euler (1707 - 1783).

Giống như số pi, số e cũng là số siêu việt có giá trị xấp xỉ 2,71828 18284 59045 23536...

Cũng như sự ra đời của các con số khác, cũng chính từ nhu cầu của cuộc sống mà cụ thể hơn ở đây là bài toán lãi kép, số e đã được sinh ra.

Chính số e cũng là con số góp phần không nhỏ trong sự phát triển của giải tích toán học,

Số thứ tám: Số ảo i

Nếu có con số nào mà sự ra đời của nó lại gây nhiều tranh cãi nhất thì đó chính là số ảo i, tên gọi của nó cũng khiến những nhà toán học bối rối khi mới ra đời.

Nếu như tất cả những con số trên là đủ để chúng ta lấp đầy trục số (thường biểu diễn là trục nằm ngang Ox trong giải tích) thì những con số đại diện cho các điểm trong mặt phẳng chỉ có thể biểu diễn khi số ảo i ra đời.

Những nấc thang được xây dựng từ các con số cơ bản.

Nghĩa là chúng ta có thể biểu diễn không chỉ giới hạn trong trục Ox mà toàn bộ mặt phẳng Oxy.

Số ảo i là giá trị của căn bậc hai của - 1. Thật khó hiểu khi một số âm lại có căn bậc 2. Chính điều này đã gây ra một cuộc tranh cãi lớn trong giới toán học vì nó quá "ảo".

Thế nhưng chấp nhận nó, một loạt các nhánh mới của toán học đã ra đời và đánh dấu một mốc phát triển vượt bậc của toán học với sự ra đời của số phức.

Như vậy có thể thấy toàn bộ nền toán học ngày nay đã được xây dựng nên chỉ từ 8 con số nền tảng trên hay nói cách khác chúng ta chỉ cần 8 con số để có thể xây dựng nên tòa lâu đài toán học vĩ đại.